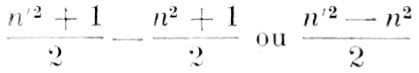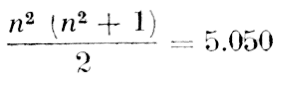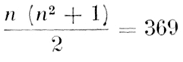Une solution arabe du problème des carrés magiques par Carra de Vaux.
Il y a quelques années je reçus de Tunis plusieurs livres arabes, parmi lesquels un traité d’el-Bouni intitulé Sharh ismellah el-a’zam, commentaire sur le grand Nom de Dieu. El-Bouni est un auteur bien connu des occultistes, originaire de Bône (Algérie), mort en 622 de l’hégire, 1225 du Christ. Son traité était édité au Caire à la Librairie commerciale Mahmoudieh, sans date. Il contenait une solution générale du problème des carrés magiques ; on sait en effet que ces carrés sont appréciés des Orientaux comme talismans.
La solution d’el-Bouni est de celles que l’on a appelées « à enceintes ». Elle peut paraître d’abord compliquée ; elle n’a pas l’élégance et la rapidité de celle que La Loubère a naguère rapportée d’après des Indiens de Sourate ; mais je crois qu’en définitive on doit la juger fort belle, parce qu’elle établit une répartition très nette des nombres composant le carré entre les enceintes successives. Je vais la donner en suivant de près le texte ; nous verrons ensuite ce que l’on peut penser de son origine.
On remarquera que pour passer de la position d’un nombre à celle du nombre suivant, l’auteur se sert volontiers de la marche des pièces au jeu d’échecs.
I. Carrés pairs
El-Bouni commence par former le noyau central, c’est-à-dire le carré intérieur de 4 cases de côté. Il place 1 dans la case à gauche de l’angle supérieur droit, et passe à 2 selon la marche du cavalier, puis place 3 et 4 symétriquement à 2 et 1 par rapport au centre. Il repart de l’angle inférieur droit, y met 5, passe à 6 en marche de cavalier, et dispose 7 et 8 symétriquement à 6 et 5.
Les 8 premiers nombres garderont cette position quel que soit le nombre n des côtés du carré à construire. Dans les 8 autres cases viendront se placer d’une façon analogue les 8 plus hauts chiffres du carré : n², n²-1,… n²-7, pris en descendant.
Cela fait, on construit la première « enceinte » ou le premier pourtour (le mot arabe est tauq, collier) qui aura 6 cases de côté. On part de l’angle supérieur droit où l’on met le 9, nombre impair ; on passe à l’angle opposé en haut où l’on met ce dernier nombre augmenté du nombre des cotés de l’enceinte moins 1, soit 9+6-1 ou 14, un pair. On descend à la case à gauche de l’angle inférieur droit, et l’on y met l’impair qui suit le 9 : 11. On remonte en haut à l’opposé de la case du roi (la voisine du 11) où l’on inscrit le 13 ; on redescend à l’opposé de la case voisine où l’on place le 15. (C’est le mouvement de zigzag.) Ainsi l’on continue jusqu’à ce que les nombres d’impairs placés soit égal an nombre du côté du pourtour moins 2 : ici 6-2 ou 4 ; pour le second pourtour 8-2 ou 6, etc.
Alors l’auteur passe à la case à gauche de la dernière qu’il vient de meubler, et il y met le nombre qui suit celui de l’angle supérieur droit, ici 10. Il se porte « en marche du fou », c’est-à-dire obliquement sur le côté gauche du pourtour, où il inscrit le pair suivant, 12. Il recommence le mouvement de zigzag, mais cette fois horizontalement, de pair en pair, et continue jusqu’à ce que le nombre des pairs placés égale aussi le nombre du côté du pourtour moins 2.
En disposant ainsi les pairs on rencontre celui qui est déjà placé à l’angle supérieur gauche (ici 14) ; il ne faut pas le répéter : on passe au pair suivant (16) qui prend sa place dans le zigzag.
Les deux derniers nombres à placer donnent lieu à une distinction : « Si le nombre du pourtour est pair-impair, (6, 10, 14…), tu continues à disposer les pairs dans le pourtour, à droite et à gauche, jusqu’à ce que tu arrives au dernier pair à placer, que tu mettras au-dessus du pair précédent, qui est toujours à droite.
« Si le côté du pourtour est pair-pair (8, 12. 16…) tu places le pair qui suit celui de la case supérieure gauche dans la case indiquée par le zigzag, qui est toujours du côté gauche, puis tu mets le pair suivant dans la case voisine au-dessus, sur ce même côté gauche ; ensuite tu te transportes à l’opposé de la case du roi (la case voisine à droite. tu y mets le pair suivant puis le suivant dans la case voisine au-dessus sur ce même côté droit ; s’il te reste des pairs à placer, tu te transportes à l’opposé de la case du roi, à gauche à la manière ordinaire, jusqu’à ce que tu en aies placé le nombre du côté du pourtour (n) moins 2 comme nous l’avons dit.
« Enfin tu places l’impair qui précède le dernier pair, sur le côté du pourtour où la moitié des rases n’est pas encore meublée, soit à droite, soit à gauche ; mais ne le mets pas en face d’une case habitée. »
Ayant ainsi rempli la moitié des cases du pourtour, on complète leurs vis-à-vis en n²+1. Le vis-à-vis d’un angle est l’angle diagonalement opposé ; le vis-à-vis des autres cases est celui de la tour.
II. — Carrés impairs
La méthode pour les carrés impairs est moins nette dans le texte publié d’el-Bouni, mais il est facile de la rétablir en partant du carré de 3 et en procédant par la différence de carrés.
A la diagonale composée des chiffres médians on ajoute
aux autres chiffres supérieurs ou chiffre médian on ajoute lu différence des carrés n’² – n² ; et les chiffres inférieurs au chiffre médian sont laissés à leur place sans changement. On complète en n’² + 1.
Ainsi pour passer du carré de 3 où 5 est le chiffre médian, au carré de 5, on ajoute à la diagonale 4, 5, 6 la demi-différence 25-2/9 ou 8. Aux autres chiffres supérieurs à 5, on ajoute la différence 25 – 9 ou 16 ; les 3 premiers chiffres ne sont pas touchés.
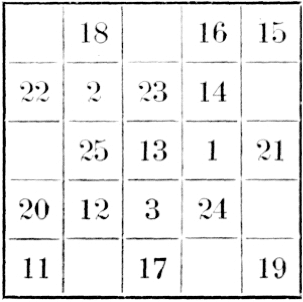
Je complète la série diagonale par 11 et 15. Je mets 10 près de l’angle 15 à gauche, et je fais le zigzag vertical 10, 17, 18. Je mets 19 dans l’angle inférieur droit, et je fais le zigzag horizontal 19, 20, 21, 22. Puis je complète les opposés en 26 : 16-10, 17-9, etc.
On ferait de même pour passer du carré de 5 au carré de 7, qui est donné incorrectement dans le texte arabe.
Somme totale des nombres :
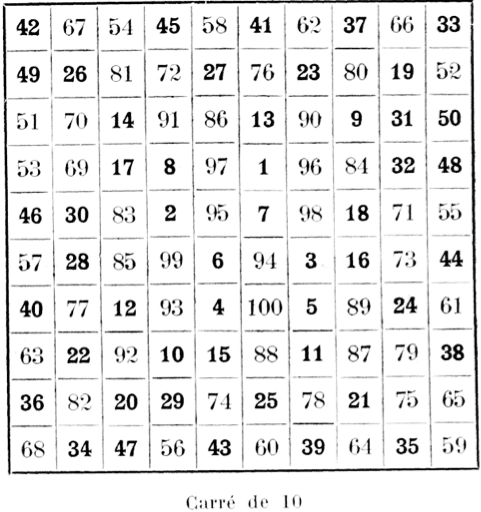
Somme de chaque ligne ou colonne : 505.
Deux nombres placés vis-à-vis l’un de l’autre sur un même pourtour donnent ensemble 101.
Le carré central contient les nombres de 1 à 8 et de 100 à 93 ; Le premier pourtour contient les nombres de 9 à 18 et de 92 à 83 ; Le second pourtour contient les nombres de 19 à 32 et de 82 à 69 ; Le troisième pourtour contient les nombres de 33 à 50 et de 68 à 51.
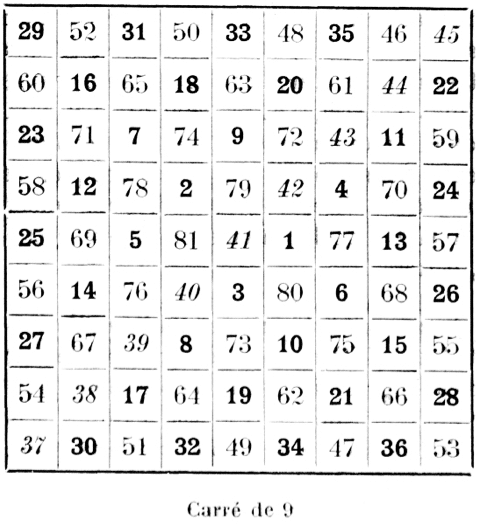
Somme de chaque ligne ou colonne :
Somme de deux vis-à-vis sur le même pourtour : n²+1=82. Une diagonale contient les 9 nombres médians de 37 à 45 dans leur ordre.
Le carré central de 3 contient les nombres de 1 à 3 et de 81 à 79.
Le premier pourtour les nombres de 1 à 10 et de 78 à 72.
Le deuxième pourtour les nombres de 11 à 21 et de 71 à 61.
Le troisième pourtour les nombres de 22 à 36 et de 60 à 46.
J’ai appelé cette solution « arabe » parce que je l’ai trouvée dans un livre arabe ; mais est-elle vraiment d’el-Bouni lui-même ? Je ne le pense pas. D’abord il ne le prétend pas ; ensuite cet auteur est surtout connu pour des travaux sur les talismans, la cabbale, les vertus des noms divins ou d’oraisons diverses : il est peu probable qu’un « spécialiste » de ce genre ait été capable de résoudre un problème aussi difficile et exigeant une si rare ingéniosité.
La rédaction peut être d’El-Bouni. Il a dû avoir une source persane à en juger par les allusions nombreuses au jeu d’échecs qui était fort en honneur en Perse. Les pièces de ce jeu sont désignées par leurs noms persans : skâk, le Roi ; roh-h, la Tour ; ferzâneh, l’intelligent, le sage, chez nous : le fou.
Faut-il aller plus loin, des Persans remonter jusqu’aux Grecs, comme on a souvent occasion de le faire quand on s’occupe des sciences orientales ? El-Bouni lui-même semble nous y inviter. Il a des expressions comme wa gis, et mesure, et compare, à la fin d’une explication, que l’on trouve dans des traités grecs antiques. Plus précisément il termine son chapitre sur les carrés magiques par cette recommandation : « Sache que le mieux est d’écrire ces carré numériques avec le qalam naturel, car c’est le qalam des sages antérieurs, et tous leurs livres et toutes leurs œuvres sont tracés avec lui. »
Le mot pour sages est hukama qui s’applique d’ordinaire aux savants de la Grèce antique ; l’épithète motakaddimount précédents, antérieur, nous reporte à la même époque. La solution des carrés magiques a dû être tenue secrète dans quelque société de savants, car à la fin de l’opuscule on relève cette apostrophe : ajuhâ lakha, ô frère !
Ozanam dans ses Récréations mathématiques et physiques (Paris, 1778, t. 1, ch. XII) a un long chapitre sur les carrés magiques. Pour les carrés impairs il donne la méthode de La Loubère ; pour les carrés pairs il donne 3 méthodes dues à des chercheurs « modernes » c’est-à-dire du XVIIe ou du XVIIIe siècle, comme Frenele et La Hire. La troisième de ces méthodes est à « enceinte », mais très différente de celle d’El-Bouni. Selon Ozanam, l’origine grecque antique des carrés magiques est certaine : « Les anciens, dit-il, ne nous ont transmis aucune règle générale, mais seulement quelques exemples de quarrés pairs rangés magiquement, comme ceux de 10, de 30, de 64 cases ».
Pour les Byzantins, on peut voir le mémoire de Paul Tannery sur Nicolas Rabdas (t. IV de ses Mémoires).
Plus sur le sujet :
Une solution arabe du problème des carrés magiques. Carra de Vaux. Revue d’histoire des sciences, Année 1948, Volume 1, Numéro 3 p. 206-212